Mary Rose Cook

For the last six months, I’ve been writing Pistol Slut, a 2D shoot-em-up in JavaScript. In this article, I’ll talk about how I solved some of the nastier problems with detecting collisions between 2D objects, specifically: bullets, grenades, exploding barrels, buildings and people.

You might find it helpful to play Pistol Slut before you read on, so you have a context for the things I talk about.

I will not be talking about per-pixel collision detection. And I will only be talking about objects whose shapes can be roughly approximated to a rectangle.

Most of the examples in this article will be conducted in pseudo-code. If you want to see the code I actually used, go and look at the repository for Pistol Slut. Both it, and the framework it is based on, The Render Engine, are open source under the MIT license. This means you can take the code and use it in any project, commercial or non-commercial, open source or not.

This article will begin with the general approach to collision detection. It will then go into special cases that solve some of the trickier problems.

Grids

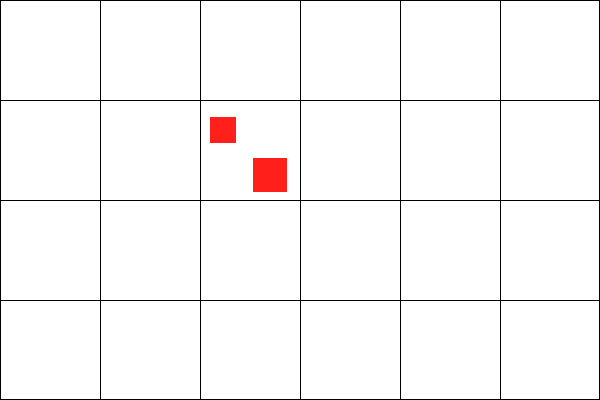
Imagine the whole game world split up by a grid. If two objects are in the same square of the grid, we assume they are colliding, like these two red squares.

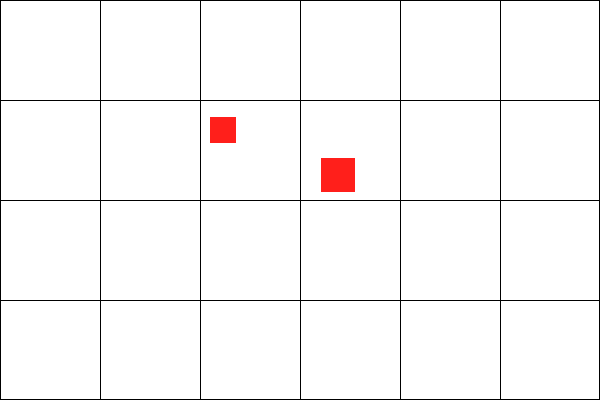
Whereas, these two red squares are not colliding:

So, to detect whether a particular object is colliding with another one in our simple little world, we can use this code:

What if the world looks like this?

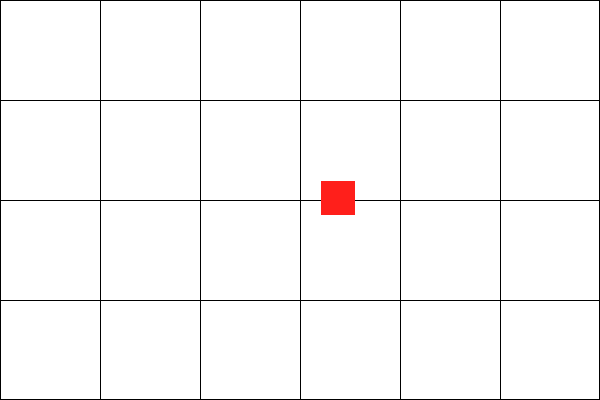
Uh-oh.

An object might exist in more than one grid square. How about we get the coordinates of all four corners of each object and add the object to the grid square containers into which the coordinates of those corners fall? No, that’s not going to fly, either, because the world might look like this:

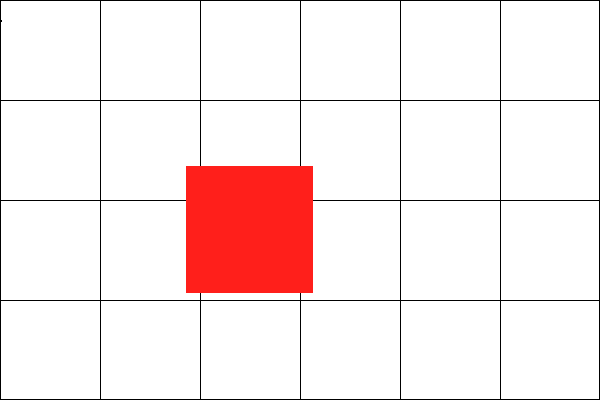
There are two solutions. Solution one, use bounding boxes, the subject of the next section. But we don’t really want to do that, because the grid is supposed to be a super-quick triage that dramatically cuts down the number of collisions we have to test further. Solution two, assume that an object will never be bigger than a grid square and, therefore, we can just add it to the grid square container into which its top left corner falls, and the containers of the eight surrounding squares. To make this happen, we can modify the second block in the previous code, giving us:

One last thing: what happens if an object moves? It might have moved to a new grid square. It’s no big deal:

Bounding boxes

We can now get a list of all the objects that a particular object is colliding with. But that’s kind of lies, isn’t it? Though the two red squares in the first diagram are occupying the same grid square, they aren’t actually colliding. Grid square co-habitation is only the first step. The next is to find out whether an object is actually overlapping another object, like these two love-birds:

We do this with bounding boxes. A bounding box is a square that is as tight a fit as possible around the actual boundaries of an object. A bounding box is defined by the x and y coordinates of its top left corner and the x and y coordinates of its bottom right corner. If two objects’ bounding boxes overlap, those two objects are colliding. To calculate if two bounding boxes overlap, we run four tests that would confirm the boxes *don’t* overlap. If all four tests come back false, the boxes are overlapping:

To get all the objects that a particular object is colliding with:

Putting it all together

The object’s reaction may depend on what type of object it has collided with. Its decision about whether it wants to hear about more objects in its grid square in this tick might depend on whether its reaction involved it being destroyed. If it is destroyed, it will probably remove itself permanently from the pool of objects in the grid.

Special cases

This is the tougher stuff. I’ll talk about how to deal with fast-moving objects, objects that can stand on top of others, objects that can push others and objects that bounce.

The root cause of most of the difficulties is the fact that objects can move several pixels per tick. Thus, you do not always hear about collisions until after one object is well inside another. Thus, it’s sometimes hard to tell at what coordinates the impact occurred. I’ll take some objects from Pistol Slut, explain the difficulties with each object, and the solutions.

Bullets

Problem one: in a tick, bullets can pass right through objects they should be colliding with. Solution: make sure they can’t ever move at a pixel speed higher than your narrowest object. You could do this by taking care to build objects that aren’t too narrow, or put a speed limit on bullets that is based on the width of your narrowest object.

Problem two: it’s hard to tell at what coordinates a bullet entered a dustbin, which makes it difficult to show the point of impact with a shower of sparks. Solution: extrapolate back through time. I have no idea what this technique is really called.

Here is a red dustbin with a red bullet being shot at it. It passes through positions A, B and C in that order.

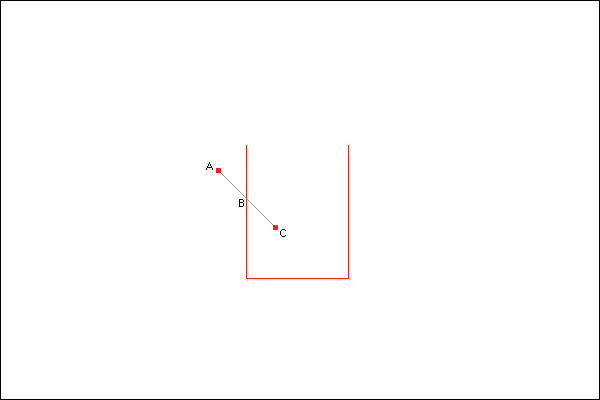
Unfortunately, ticks only occur when the bullet is at positions A and C. Therefore, with the system outlined above, the bullet won’t know about a collision until it reaches position C. That will be fine for destroying the bullet to represent the fact that it has hit the dustbin, but it won’t be so great for doing the beautiful shower of sparks. If we drew those sparks at point C, the location of the bullet when we detected the collision, they would look like this:

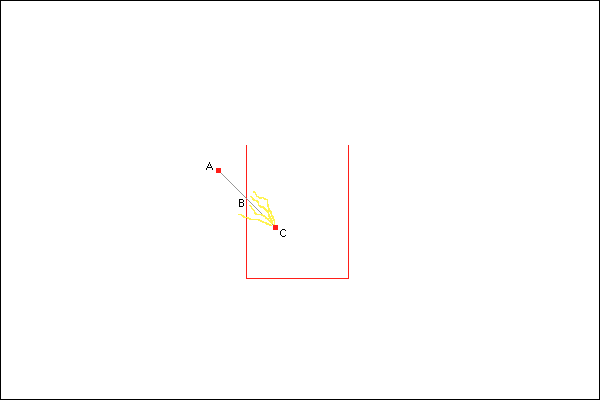
Lame.

We need to find position B. That way, the sparks will originate from the point of impact. As a bonus, I will show you how to make the sparks go in the right direction.

For the first part, draw an imaginary green line between position C and position A. That is, a line between where the bullet is now and where the bullet was in the previous tick. Then, draw four more imaginary purple lines, one along each side of the bounding box of the dustbin.

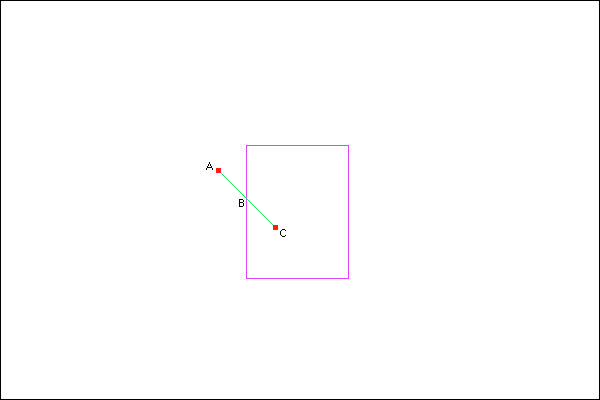
The move is to find out which bounding box line the C to A line intersects, and where. Here are two JavaScript functions; the first tells you if a line between p1 and p2 and a line between p3 and p4 are intersecting and the second tells you where.

So, with the power of maths in our hands, we can now figure out where position B is:

And, thus, emit the shower of sparks from that point.

But in which rough direction should the sparks go? Ack. Start crying: here comes some more maths.

reverseAngle() is the key function, here. It gets the normal to the side of the dustbin that the bullet hit. That is, it gets the outward-facing line that is perpendicular. It gets the angle between the normal and the bullet’s vector and then spins that angle around to adjust it to the direction appropriate for the side that was hit. The result is the angle the sparks should go along.

Grenades

Problem one: grenades bounce. Solution: use the code from the Bullets section to get the point of impact of the grenade and then reflect the angle of impact and send the grenade off in this new direction. And maybe reduce the grenade’s velocity a little to account for friction and the fact that grenades aren’t exactly like super balls when it comes to bouncing. Easy.

Problem two: solution one was a bit of a lie. The reflect direction stuff we used for bullets will still work great with grenades, but the stuff with using the grenade’s current and previous positions to get its trajectory and, thus, where it hit the dustbin, can be problematic. It’ll work most of the time, but not all. I’ll explain why.

When we drew the imaginary line between the current and previous positions of the bullet, we drew it between the top right hand corners of the two positions. This is fine, because the bullet actually IS only a single point. It’s drawn as a single pixel. But grenades are bigger than that. So, something like this might happen:

The first time we hear about a collision with the red dustbin will be when the red grenade is at position C. However, though the lower right portion of the grenade is intersecting with the dustbin at position C, the line we draw between the top left corners of each position does not, and will never, intersect with the dustbin. There is no position B. Thus, we will not get a point of impact and, thus, we won’t know where to bounce the grenade from.

But, fear not. We can solve this problem. We could draw lines between each corner of the previous and next positions: top left to top left, top right to top right, and so forth. However, there is a more elegant, more general solution: sweeping.

This solution has two cases. In the first case, at a particular tick, the red grenade is intersecting the side of the red dustbin:

In this case, the code to get the angle to bounce the grenade is straightforward:

To determine whether a line intersects a box, make a rectangle of the line and then see if that rectangle overlaps the box rectangle. To make a rectangle from a horizontal or vertical line between p1 and p2:

In the second case, the red grenade is already fully inside the dustbin:

To deal with this, we use a technique called sweeping. The idea is to move the grenade back along its trajectory in small increments, testing at each position to see if it is overlapping any of the sides of the dustbin. Like this:

The initial collision is detected when the grenade is at position A. We then sweep its position back incrementally to positions B, C and D, testing to see if it collides with any of the edges of the red dustbin. We finally get a hit at position E.

To handle both this case and the previous case, we can write this code:

People

What is special about people? They can bump into and stand on top of things. To handle these scenarios, we can write this code:

And to figure out whether the girl is falling or rising or walking through the dustbin, we can write this code:

Exploding barrels

Exploding barrels are not so notable for their explodeyness as for the fact that they can be pushed. Using the code we are already using for the girl, we can handle this:

Artificial intelligence

That’s it for the collision detection in Pistol Slut. Well done. My next article will be about artificial intelligence with state machines.